What is a Tree?

In computer science, a tree is a hierarchical data structure composed of nodes.

• Every tree has a root node.
• Nodes may have children (left, right).
• A node without children is called a leaf.
• The height of the tree is the maximum distance from the root to a leaf.
• The depth of a node is the distance from the root to that node.

In simple words: think of a tree as a folder with subfolders inside other subfolders.

---

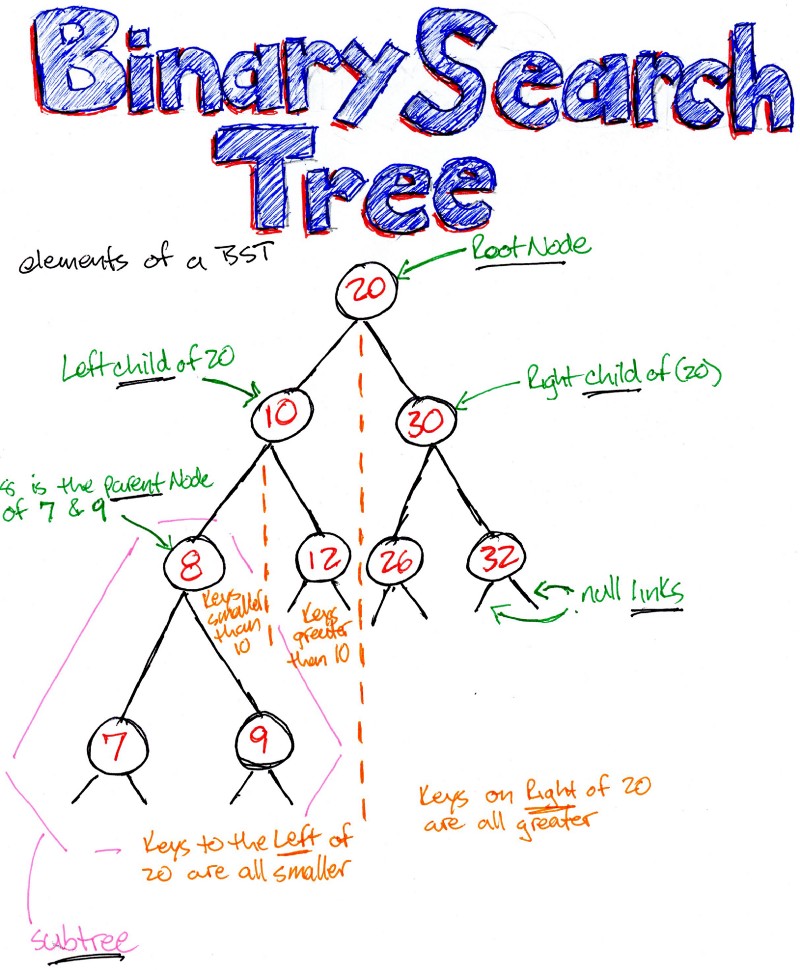
Binary Search Tree (BST)

A Binary Search Tree (BST) is a special type of binary tree where:

• Values smaller than the current node go to the left.
• Values greater go to the right.
• This allows searches, insertions, and deletions to be more efficient than in a list.

Example inserting [5, 3, 7, 2, 4] in a BST:

    5
   / \
  3   7
 / \
2   4

---

---

Inserting into a BST

The logic of insertion in a BST is:

1. If the tree is empty, the first node becomes the root.
2. If the value is smaller than the current node, go left.
3. If the value is greater, go right.
4. When an empty spot is found, create the new node there.

Java code with Recursion:

if (root == null) root = new Node(value);
else if (value < root.data) insert(root.left, value);
else if (value > root.data) insert(root.right, value);if (value > root.data) insert(root.right, value);

// Class representing a tree node
class Node {
    int data;      // value stored in the node
    Node left;     // reference to the left child
    Node right;    // reference to the right child

    public Node(int data) {
        this.data = data;  // initialize the node with a value
    }
}

public class BinaryTree {
    Node root;  // root of the tree (null if empty)

    // Public method to insert a value into the tree
    public void insert(int data) {
        root = insertRecursive(root, data); // delegate to recursive method
    }

    // Recursive insertion
    private Node insertRecursive(Node rootNode, int data) {
        // Base case: if no node here, create a new one
        if (rootNode == null) {
            return new Node(data);
        }

        // If smaller, insert into the left subtree
        if (data < rootNode.data) {
            rootNode.left = insertRecursive(rootNode.left, data);
        }
        // If greater, insert into the right subtree
        else if (data > rootNode.data) {
            rootNode.right = insertRecursive(rootNode.right, data);
        }

        // Return the current node unchanged
        return rootNode;
    }

    // Public method for in-order traversal
    public void inOrder(Node root) {
        inOrderRec(root);
    }

    // In-order traversal (Left → Node → Right)
    private void inOrderRec(Node root) {
        if (root == null) return; // base case: empty node

        inOrderRec(root.left);             // traverse left subtree
        System.out.print(root.data + " "); // visit current node
        inOrderRec(root.right);            // traverse right subtree
    }
}

---

Visual Example: How does the stack work in an In-Order Traversal?

First, let’s recall what: In-Order Traversal means:
In a Binary Search Tree (BST), the In-Order traversal visits nodes in this order:

1. Traverse the left subtree.
2. Visit the current node (root).
3. Traverse the right subtree.

---

Step by Step with the Stack

    5
   / \
  3   7
 / \
2   4

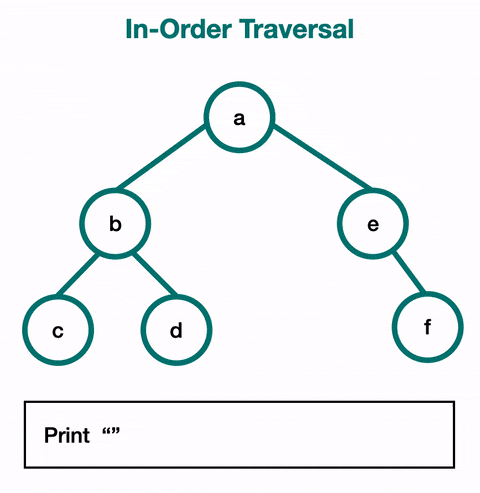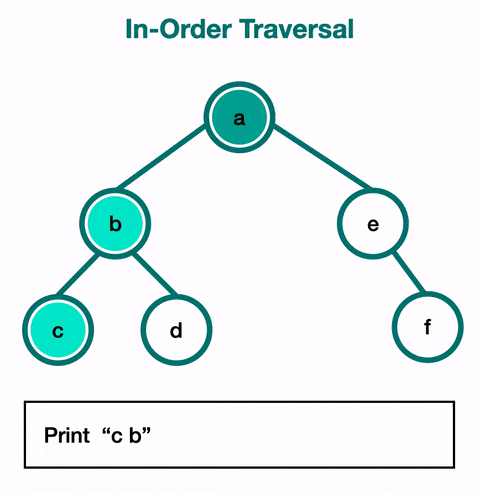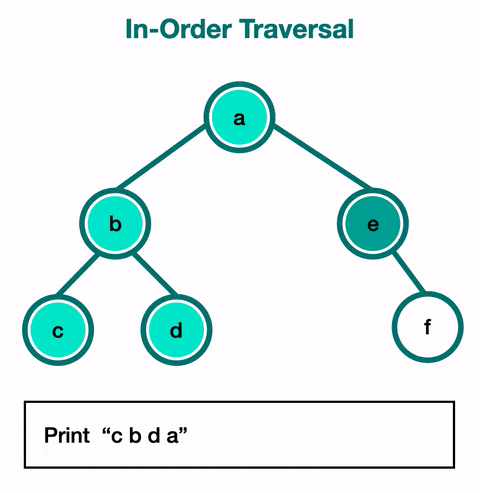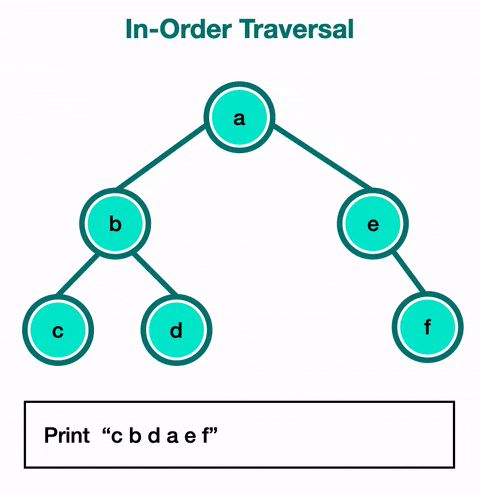
1. Start at root (5). There’s a left child, go down: Stack: [5]

2. Reach 3. Still has a left child, keep going: Stack: [5, 3]

3. Reach 2. No left child, visit it (print it). Output: 2
   Stack: [5, 3]

4. Back to 3. Visit node. Output: 2 → 3
   Stack: [5]

5. Explore right child of 3 → 4. Visit it (no children). Output: 2 → 3 → 4
   Stack: [5]

6. Back to 5. Visit node. Output: 2 → 3 → 4 → 5
   Stack: []

7. Explore right child of 5 → 7.
   Visit it (no children). Final Output: 2 → 3 → 4 → 5 → 7

---

Final Result

The In-Order traversal of this tree returns the elements in ascending order:

👉 This guarantees the values are visited in sorted order.

---

Important Note: Theory vs. Production Practice

A BST works very well as an academic concept or for in-memory structures (RAM), where some tree height is acceptable.

But in production environments with real data (databases, file systems, disk storage, S3, etc.), using a raw BST is not efficient:

• It can become unbalanced and very tall (degrading operations to O(n)).
• Accessing disk data involves multiple costly jumps if the tree is deep.

That’s why in practice, we use balanced and disk-optimized structures, such as:

• AVL / Red-Black Trees → when dynamic balance is needed in memory.
• B-Trees / B+ Trees → in file systems and SQL databases.
• HashMaps → in memory, for very fast key-based access (like caches).

B+ Trees in SQL and Databases

When talking about database engines like MySQL, PostgreSQL, or Oracle, one of the heroes behind efficient search is the B+ Tree.

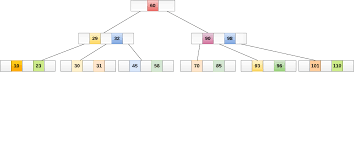
What is a B+ Tree?

A B+ Tree is a balanced tree variant designed specifically for disk storage. Unlike BSTs or AVL trees, B+ Trees:

• They have multiple keys per node (not just one).
• Each node can have many children, reducing the height of the tree.
• All the real keys (data) are located in the leaves.
• Internal nodes (including the root) store only keys and pointers to guide the search; the actual data/rows are only in the leaves.
• The leaves are linked together like a linked list, which allows easy traversal of the data in ranges.

Advantages in SQL

1. Lower height = fewer disk accesses
   Each access to a node in a tree stored on disk implies a costly page read.
   By allowing more keys per node, the B+ Tree keeps the height very low and optimizes searches.

2. Efficient ranges (BETWEEN, ORDER BY)
   Thanks to the fact that the leaves are linked, performing a range query (WHERE id BETWEEN 100 AND 200) becomes simply traversing that list of leaves, without needing to climb back up the tree.

3. Indexes in SQL
   Most database engines implement their indexes using B+ Trees.
   When you create an index on a column (CREATE INDEX ...), you are actually building a B+ Tree that organizes those values for fast lookups.